.jpg)
无规行走模型的应用范围很广，酒鬼漫步失足悬崖的问题也有许多不同的故事版本，但描述的数学模型基本一致。比如说，赌徒破产问题是其中一例。
（图片来自网络）
说的是有赌徒在赌场赌博，赢的概率是p，输的概率1-p，每次的赌注为1元，假设赌徒最开始时有赌金n元，赢了赌金加一元，输了赌金减一元。问赌徒输光的概率是多少？这个问题与上面解决的酒鬼悬崖问题的数学模型完全一样，赌金的数目对应于酒鬼漫步中的1维距离x，悬崖位置x=0便对应于赌金输光赌徒破产。从上面分析可知，即使p=1/2，酒鬼也必定掉下悬崖。赌徒问题中赢的概率p=1/2对应于公平交易，但事实上赌徒与赌场赢的概率比是（49:51）。即便是公平交易，与酒鬼类似，赌徒最终仍然破产，无论你最初有多少赌金，因为你的赌本毕竟是有限的，而你的博弈对手（赌场）理论上而言拥有无限多的赌本。
酒鬼失足（或赌徒破产）问题还可以稍加变换构成一些新型的趣题。比如说，假设酒鬼的路上两边都有悬崖，计算分别掉到两边悬崖的概率。赌博问题上，便相当于两个赌徒A和B赌博，看谁先输光。有一个“网球比赛的输赢问题”，也是基于类似的数学模型。
（图片来自网络）
也可以假设酒鬼的路上根本没有悬崖，且路的两头都可以无限延伸，酒鬼从自家门口出发，要你计算，酒鬼出去漫游之后，最后还能够回到家的概率等于多少？
上面的所有例子，涉及的都是最简单的1维无规行走问题。从1维可以扩展到2维、3维以致更多的维数。但是，有时候并非简单的扩展，比如上面那个“酒鬼回家”的问题，空间维数不一样的时候，答案却大不一样。
首先看看1维的情况：酒鬼随机游走在长度无限的路上，时左时右，但只要时间足够长，他最终总能回到出发点。因此，回家的概率是100% 。二维的情形也类似，相当于酒鬼从家里出发，游走在街道呈方格网格状分布（设想为无限大）的城市里，他每走到一个十字路口，便概率均等地从4个方向（包括来的方向）中选择一条路（图3-2-1a）。和1维的情况类似，只要时间足够长，这个醉鬼总能回到家，概率仍然是 100% 。
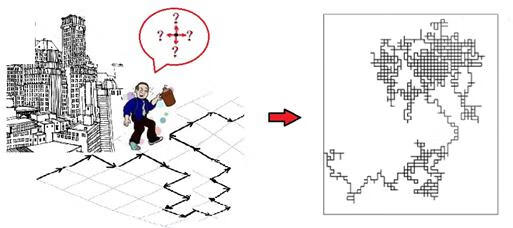
图3-2-1：酒鬼漫步和二维无规行走路径
有一个颇为著名的美籍匈牙利犹太裔数学家波利亚（George Pólya，1887年－1985年）认真研究了这个“酒鬼能否回家”的问题，刚才所说的在1维2维情况酒鬼回家概率等于100%便是被他在 1921 年证明的。波利亚二战时移民美国，后来是斯坦福大学教授。
“酒鬼能否回家”问题的1维2维答案不足为奇，波利亚令人吃惊的贡献是证明了这个问题在维数更高的情况下酒鬼回家的概率大大小于1！比如说，在三维网格中随机游走，最终能回到出发点的概率只有 34% 。
图3-3-1：“酒鬼小鸟回家”定理
酒鬼不可能在空中游走，鸟儿的活动空间才是3维的，因此，美国日裔数学家角谷 静夫（Shizuo Kakutani，1911–2004）将波利亚定理用一句通俗又十分风趣的语言来总结：喝醉的酒鬼总能找到回家的路，喝醉的小鸟则可能永远也回不了家。
无规行走也是物理学中布朗运动的数学模型，欲知详情，且听下回分解。
（摘自《从掷骰子到阿尔法狗：趣谈概率》，作者：张天蓉）
相关推荐
-
永恒之塔新手礼包在哪领(永恒之塔2022哪些礼包)
《AION》是韩国的NCSOFT推出的另一款在线游戏，虽然画面和场景和《天堂2》同样走精致奇幻风格，但是在游戏性的设计上，则更强调“玩家影响世界，世界影响玩家”的互动循环关系，玩家将可更深入感受到自己是整个游戏世界的一份子。究竟要如何表现这样的互动变化呢？例如一个村庄里面只有两个店铺，如果其中一个店
-
tnt海盗战舰(tnt轰炸机)
对于《我的世界》这款沙盒游戏，相信很多玩家都有一些了解，毕竟至今为止，它已经运行了13年之久，里面玩法也是渐渐的趋于平静，因此可以一直提供新鲜感。不过玩家们要是想跟，实力强大的怪物交手的话，“腐烂生物”MOD或许是最好的选择，制作者在其中，创建出了多种不同的僵尸变种，实力均十分强大，如果不加以防范的
-
修罗道ol吧(修罗道ol怎样玩才厉害)
《火影忍者ol》游戏中，经过改版后，都有平民阵容还可以用，下面就和小编一起来看看火主篇平民阵容盘点。1、火秘技：火主色鹿忍牙忍志乃。通灵蜥蜴。前期火主最强阵容，没有之一，很容易入手，开服2天就能集齐，后期也能用用2、火佩恩队：人间道，修罗道，蝎，高连击加上修罗道的点燃，蝎的毒，人间道的定身伤害很高3
-
青丘狐传说小说漫画(青丘狐传说内容介绍)
额，为啥今天迷之三百字会放在上午写呢？你猜？你再猜？你再再猜？约会？电影？吃饭？NONONO，都不对，告诉你们，是因为，嗡爷还没睡，啊哈哈哈哈，想不到了吧？我可是一夜七次狼，嗷呜嗷呜嗷呜～～～，哈哈哈。其实吧，我是怕一会睡着了晚上起不来更新，啊哈哈哈，猜不透吧，让你们猜透了，我还是嗡爷么，服不服！？
-
怪物史莱克2下载(怪物史莱克4国语下载)
《斗罗大陆-神界传说2》是一款唐家三少正版IP授权斗罗玄幻神战手游，还原原汁原味的斗罗神战世界！神界危机降临，光明神祗与黑暗神祗正式决裂，唐三、小舞、五大神王、史莱克七怪等经典角色乱世沉浮，上演最强斗罗巅峰之战！神魂融合技破碎虚空，绝世暗器击穿混沌，百变时装战力爆表......这就是《斗罗大陆-神界
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请通知我们，一经查实，本站将立刻删除。