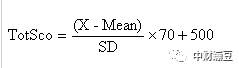.jpg)
方程法适用于绝大部分题目，可以说是数学运算题的通用方法，基本的解题思路可以表示为“审题——设未知数——根据等量关系列方程——解方程”。
1.设未知数
(1)利用比例、倍数关系设未知数
当两个未知量之间存在比例、倍数等关系时，通常可设其中一个量为未知数，根据上述关系表示出另一个量。
(2)取中间量设未知数
当题干含有多个未知量时，这些未知量之间往往具有等量关系，或与某一中间量存在数量关系，此时可设中间量为未知数，由此表示出其他的未知量，减少未知数的个数。
2.根据等量关系列方程
在使用方程法解题时，关键是要从题干条件中找到在数量上相等的一种关系，即等量关系，通过这种等量关系，我们可以列出方程，进而求解未知数。
3.解方程
(1)一元一次方程
解一元一次方程有五步，即“去分母、去括号、移项、合并同类项、系数化为1”。
(2)多远一次方程
多元一次方程一般通过代入消元或加减消元法求解。
在行测考试中，由于题目的设置，往往不需要求出方程组中所有未知数的解，此时，可以使用换元法，即把某一部分视为一个整体进行运算。
换元法的基本解题步骤为“设元-换元-解元-还元”。
设元-换元：当不同方程中出现相同的部分时，可将相同部分看作一个整体进行计算。
解元：对应解出换元后的未知数。
还元：将所解结果还原成所求未知数的形式。
(3)不定方程
方程中未知数的个数多于等式个数，我们称这样的方程为不定方程。不定方程无法使用常规方法求解，需要运用整除特性、奇偶性、尾数、特值等结合选项判断正确答案。
奇偶性
性质1：偶数±偶数＝偶数，偶数±奇数＝奇数，奇数±奇数＝偶数。
性质2：偶数x偶数＝偶数，偶数x奇数＝偶数，奇数x奇数＝奇数。
推论1:奇数个奇数的和是奇数;偶数个奇数的和是偶数。
推论2:几个数的乘积如果是奇数，那么这几个数一定都是奇数;几个数的乘积如果是偶数，那么这几个数中至少有一个偶数。
推论3：两个数的“和”与这两个数的“差”奇偶性相同。
当遇到“在不同分配情况下，有剩余，或不足”的问题时，既可以列方程求解，也可直接套用盈亏问题的公式。关于盈亏问题的具体公式如下：
一盈一尽型：盈数/两次分配个数的差＝对象数
一亏一尽型：亏数/两次分配个数的差＝对象数
一盈一亏型：(盈数+亏数)/两次分配个数的差＝对象数
两次皆盈型：(大盈数-小盈数)/两次分配个数的差＝对象
相关推荐
-
考研满分到底是450还是500呢(考研满分是多少啊)
四六级证书不仅是英语能力的衡量指标，更是学习能力的衡量指标。小编很坚定的告诉你，四六级很重要，至少你必须通过四级。四六级考试分数是这样算出来的……根据全国大学英语四六级考试委员会官网公布的消息，大学英语四、六级考试（CET）分为四级（CET-4）和六级（CET-6）两个级别。大学英语四、六级考试的分
-
大脑开发程度(人的大脑如何开发)
不知道什么时候，我就听到了这样一句话：“普通人的大脑只开发了10%，如果我们可以开放其余的90%，那你我都可能会是天才”。这句话最早起源于西方神经外科医生对大脑的研究论文，但这并不是严谨可靠的文献，人类对大脑的认识还很肤浅。这种没有实证但看起来如此励志论文落到某些作家的手中就更加肆无忌惮地传播了。最
-
关于我的老师的作文300字(怎么写一篇我的老师作文)
篇一：我最敬爱的老师在我学习的旅途中，我最敬爱的老师就是我四年级的华文老师——黄老师。她身材中等，有时还带着一副眼镜，使她看起来有一点严肃。但是上了她的课之后，我觉得她性情温和。如果我们做错了事，她一定会尽力劝我们，好言规劝，要我们改过自新。当我们向她请教功课时，她会耐心地指导我们，直到我们明白为止
-
商务英语口语(商务接待英语口语)
常用的商务英语口语有哪些?小编总结了一些，希望可以帮到大家。Are there any discount tickets for me 给我有折扣吗？ It’s all personal effects. 这些东西都是我私人用的。 From which station does the trai
-
带龙成语有哪些(带龙带虎带猴的成语)
疯狂猜成语四条龙成语答案。游戏中仔细观察会发现图中四个繁体字龙都缺少个立字，正是群龙无首。释义：一群没有首领的龙。比喻没有人领导，事情无法进行。各位玩家想必已经猜到疯狂猜成语四个龙指的就是群龙无首这个成语了。群龙无首〖解释〗：一群没有首领的龙。比喻没有人领导，事情无法进行。〖词性〗：贬义词〖示例〗：
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请通知我们，一经查实，本站将立刻删除。