学好应用题是小学生学好数学的关键，如果应用题学不好，不仅小学数学学不好，连中学以后的数学，也都不可能学好了。而学会分析，又是学好应用题的关键步骤。

老黄的应用题五步法(审题——分析——解题——反思——拓展)，第一步审题是基础，前面已经介绍过了。今天老黄就要给大家讲一讲解应用题的关键一步——分析。

分析的核心是分析方法的应用。分析的方法有很多，每个人掌握的种类也不同，按照自己的思维方式，命名和理解都可能有所不同。老黄按自己的理解，将分析方法罗列如下：

公式法、方程法、直观分析法、图例法、列表法、图表法、图像法、函数法、逻辑推理法、逆向思维法、反证法、特值法、检验法、排除法、总结规律法、模拟实验法、极端假设法、情景迁移法、建模法和构造法等。不一罗列，有一些方法一时之间也想不起来。

当然，作为中小学生，不可能掌握所有这些分析的方法。小学生主要是掌握公式法、方程法、直观分析法、一些特殊的图例法和列表法。而到了中学就要掌握绝大多数的方法。这些方法也不是绝对的孤立的，它们是经常结合起来使用的。而且也不是说某些方法就是比较低级的、容易的，某些方法就是比较高级的、困难的。而是每种方法都有它的低级形态和高级形态的。由于篇幅太长，下面老黄就只对各个分析方法做一个简单的介绍。

1、公式法。这是小学生最喜欢的方法。只要有公式，完成审题之后，照代公式就可以了。如求面积的公式，求体积的公式等。到了高中大学，公式就越来越多，也越来越复杂，反而会变成学生最害怕的方法。

2、方程法。这个方法大家都很熟练吧！从小学五年级开始就学方程式，到了初中，有一元一次方程、二元一次方程组、三元一次方程组、一元二次方程以及不等式方程(组)、分式方程、根式方程方程等。用它们来解决问题似乎都很得心应手，但是到了高中、大学，遇到多元高次方程，再试试就苦不堪言了。所以小学基础不打好，后面是不可能学得好数学的。

一般步骤是设未知数，找到等量关系列方程，然后解方程，检验解的正确性，就可以做答结题了。

3、直观分析法。就是把一些抽象问题直观化。最常见于关于数位的应用题。画一个一行多列的方格，每一格表示一个数位，把数位上的数，或者数与数之间的关系式填上去，再运用算术或方程法，把它算出来。

这类方法也可以归为图例法，因为直观分析，一般都要利用图例表示。当然，如果有实物，拿实物来分析，就更直观了。

4、图例法。图例有千千万万，其中最重要的一类图例分析法，就是线段图分析法。相信大家都有接触过。这类方法是最普遍，也是最重要的，一定要掌握起来哦。

5、列表法。比如分析二元一次方程的解，就一定要用到列表法。还有作函数的图像时，要用到列表法。列方程时也经常用到列表法。当然还有概率问题。这种方法大家应该也在书里见过，或者看过老师演示的。

6、图表法。主要用于数据统计类应用题。千万不要认为介绍的内容少，就不重要哦。

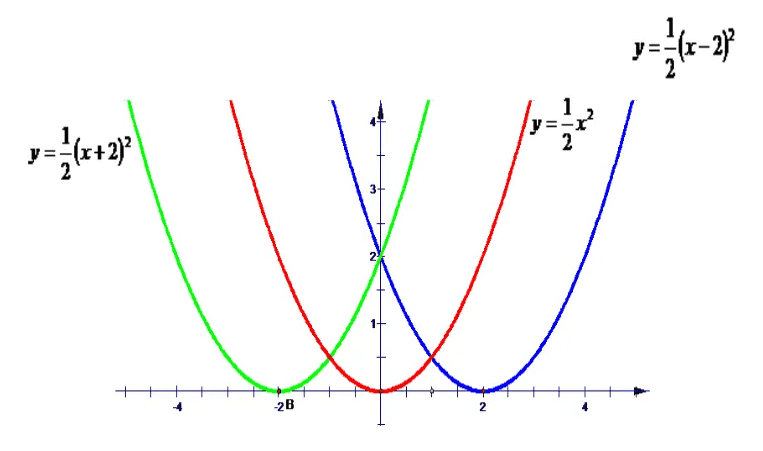
7、图像法。这是专门用来研究函数的。老黄经常说“有图有真相”，就来自于此。特别重要的一种方法。

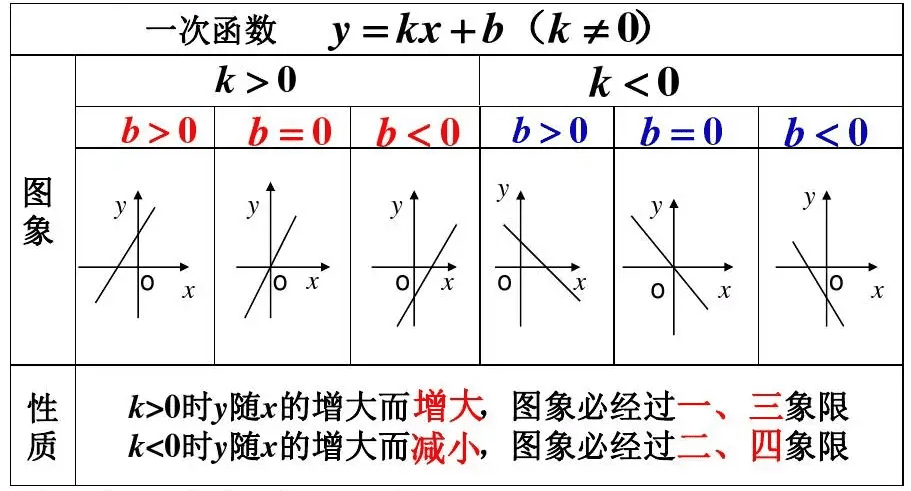
8、函数法。就是建立函数，用解决函数的思路解决实际问题。很明显的，函数法和图像法就是一对孪生兄弟。方程法则是它的堂兄弟。

9、逻辑推理法。这是用来解几何证明题、几何解答题和逻辑推理题的。

10、逆向思维法。当逻辑推理行不通时，就要学会逆向思维。逻辑推理是正向推理“因为条件，所以结论”，逆向思维是反向推理“如果有结论，那么需要什么条件”。

11、反证法。假设正确，然后证明假设正确的结论与已知条件或结论矛盾，反过来证明假设正确的结论是错误的。虽然听起来，更像一种解题的方法，但我们也可以拿它来分析问题。

12、特值法。有时候，我们需要用一些特别的数值，来检验分析的思路是否正确。比如角度问题，用平角或直角，来检验前面的思路是否存在问题的一种方法。

13、检验法。和特值法有所不同的是，检验法是通过检验一系列普通数值，以帮助我们找到解决问题的方向。

14、排除法。和检验法相反。检验法是为了检验正确的分析方向。排除法是为了检验出错误的分析方向。以上三种方法：特值法、检验法、排除法，以及下面要介绍的极端假设法最多应用于选择题。

15、总结规律。顾名思义，就是在分析过程中，为了找到某些数量上的规律，或者图形上的规律，或者运算上的规律的分析过程。它是检验法和排除法的目标。

在立体几何方面，有三类解决方法：一类是实物观察法，就是上面提到的直观分析法；还有一类就是总结规律的方法。最后一种方法就是下面要介绍的“直观想象法”。大多数人会选择总结规律。因为实物不可能想有就有，很多问题又直观想象不出来，所以只好总结规律了。

另外，所有的数学定理，公式，都可以认为是总结规律的结果。不过它们更多产生于反思和拓展的阶段。

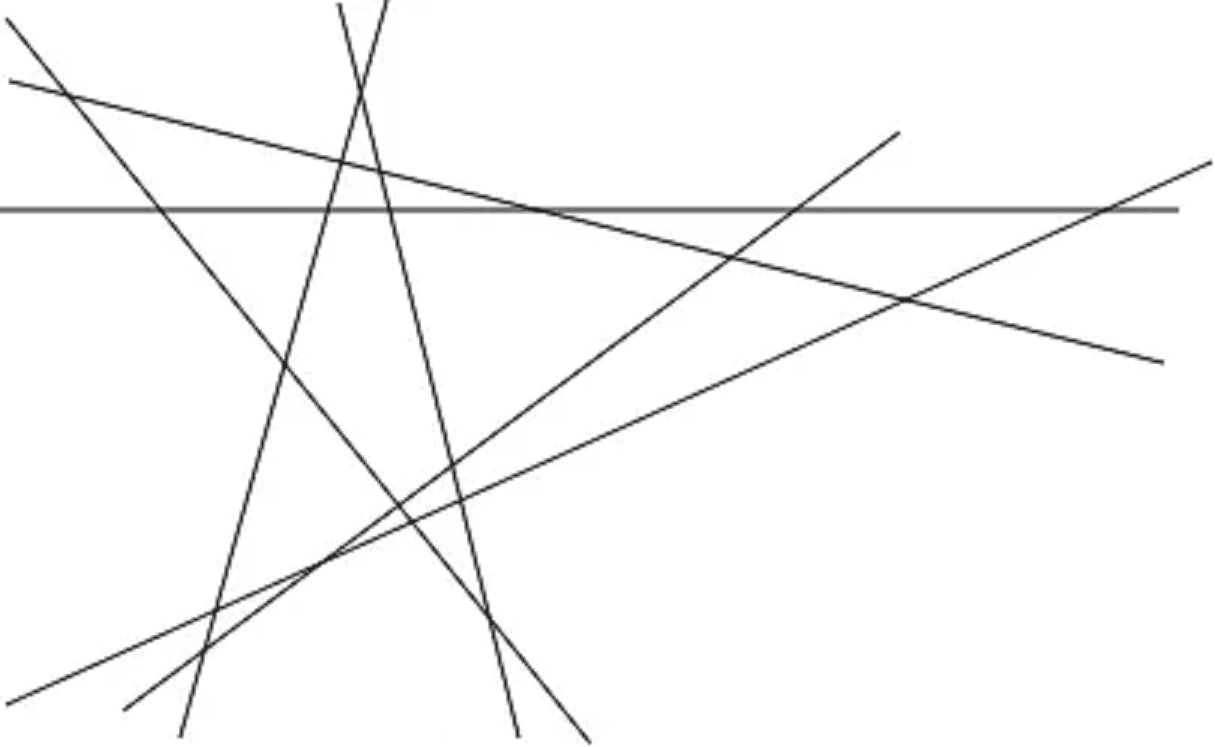
16、直观想象法。这种方法很难介绍清楚。简单地说，如果我问你，两条直线最多有几个交点，你肯定脱口而出“一个”。那三条呢？这时有些人就要想一想了。四条呢？有很多人就想不明白了。五条呢？六条呢？现在就是考验你的直观想象能力的时候了。一直到n条，你再好的直观想象都做不到了，只能用总结规律的方法来分析了。不过，任何人，都有它的直观想象能力范围的，而且这种能力是可以通过锻炼来提升的。极限就是四维空间的想象问题了。

17、模拟实验法。它是直观想象的进化版。因为直观想象的内容一般是静态的，而模拟实验的内容是动态的。当然，它也有低端版本的，就是可以借助文字、图形、表格等方式来描述的。举个简单点的例子，比如图形平移、对称等变换问题，有些就要模拟实验一下，才能解决。

18、极端假设法。其实高等数学的极限、导数、积分等知识，通通是极端假设法的产物。举个非常直观且简单的例子，但有点跑题。比如问：身上压着的东西越重，是不是身体就越受不了。你要是拿一个苹果和一个梨来做实验，肯定得不出结论的。但是如果你拿一座山来模拟实验一下。别说是人了，世界上任何一样有一定体积的动物，都会明白其中的道理了。

19、情景迁移法。这是一种特别好用的方法。就是把数学问题迁移到自己最感兴趣，最熟悉的领域上去探究。比如，幼儿园的孩子学习1+1等于多少。你跟他说，答对就奖励这个数字支棒棒糖，答错就没有。每天试一次。他就不可能不会了。

再比如，老黄小的时候学数学，都是用“元”来代替所有单位的，什么算式都是一算就准的。因为老黄从小就是一个钻在钱眼里的人。

20、建模法。就是把一类问题建立成一个模型。以上所有的方法，都是建模法的结果。它更多用于反思阶段。但也有一些人，可以用它来分析。从来没见过的题，能即时建模，都是有天才潜质的。其实很多人有天才潜质的，包括老黄自己。只不过很多人和老黄一样，都是方仲永罢了。希望孩子们不要成为这样的方仲永。

21、构造法。它是建模法的进化版。通过建模，把一类数学问题归纳进一个模型中，并设计出一套解决这个模型的方法。而构造法，就是把那些看似不在这个模型中的问题，通过数学方法进行改造，把它构造成这个模型中的一个实例的方法。

就简单的就是已知a+b=2，问-a-b等于几。看似简单地在第一个负号前面加括号，括号内要变号，得到-(a+b)=-2。但这里面就包含有构造法的思想。