.jpg)
点击上方超级数学建模可加关注
传播数学干货，学会理性的方式去思考问题
小编有话说：
最近一段时间有小伙伴跟小编吐槽题目太简单，可怜小编搜索能力有限，现向超级数学建模平台全体成员征集Think题目，欢迎各位投稿至supermodeling@163.com，欢迎来稿！
上期题目（请戳进“阅读原文”回顾）
上期答案揭晓
假设有一个三角形 ABC ，其中从 B 顶点引出 n 条射线，与 AC 边交于 n 个点，又从 C 顶点引出 m 条射线，与 AB 边交于 m 个点。所有这些线条在三角形内一共产生了 mn 个交点。现在，在每一个交点处都画一个小圆，于是每个小圆内都会有两条小线段。对于每一个小圆，我们都随机从下述三个操作中选择一个来执行。
擦去 C 点所引射线上的小线段，仅保留 B 点所引射线上的小线段
擦去 B 点所引射线上的小线段，仅保留 C 点所引射线上的小线段
擦去圆内的全部两条小线段
擦去 C 点所引射线上的小线段，仅保留 B 点所引射线上的小线段
擦去 B 点所引射线上的小线段，仅保留 C 点所引射线上的小线段
擦去圆内的全部两条小线段
三种操作各自被选中的概率分别为 p 、 q 和 1 – p – q 。于是，每一个小圆里都最多只留下了一条小线段。
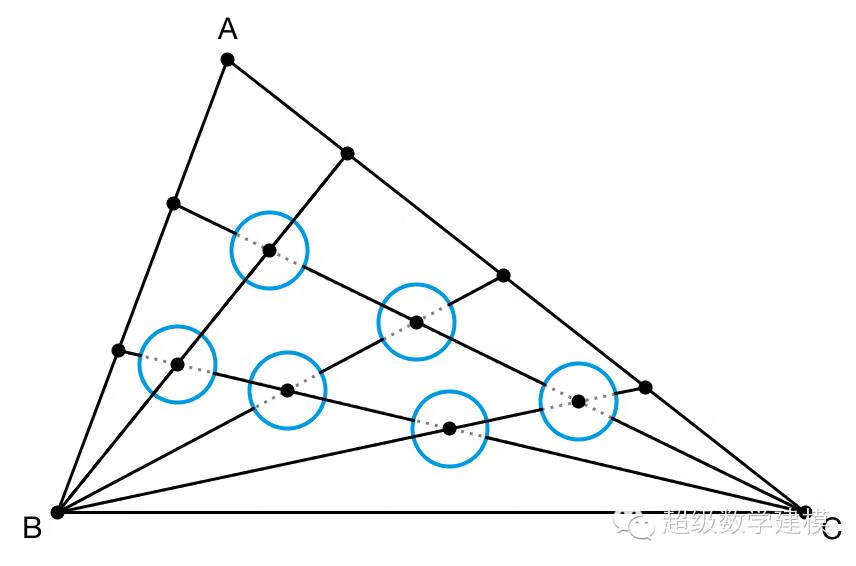
每条从 B 点出发的线上都有 m 个小圆，这条线在 m 个小圆内都被保留下来了的概率是 pm ，因而整条线有断掉之处的概率就是 1 – pm 。从 B 点出发的线一共有 n 条，每条线都有断掉之处的概率就是 (1 – pm)n 。因此，至少有一条线完好无缺的概率就是 1 – (1 – pm)n 。类似地，从 C 点出发的 m 条线当中，至少有一条线完好无缺的概率就是 1 – (1 – qn)m 。
但是，从 B 点出发的线条只要有一条是完全连通的，都会使得从 C 点出发的所有线条都断掉；从 C 点出发的线条只要有一条是完全连通的，都会使得从 B 点出发的所有线条都断掉。因此，存在某条从 B 点出发的完好的线，与存在某条从 C 点出发的完好的线，这两个事件是互斥的。这说明
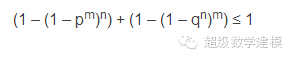
整理可得
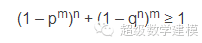
今日问题
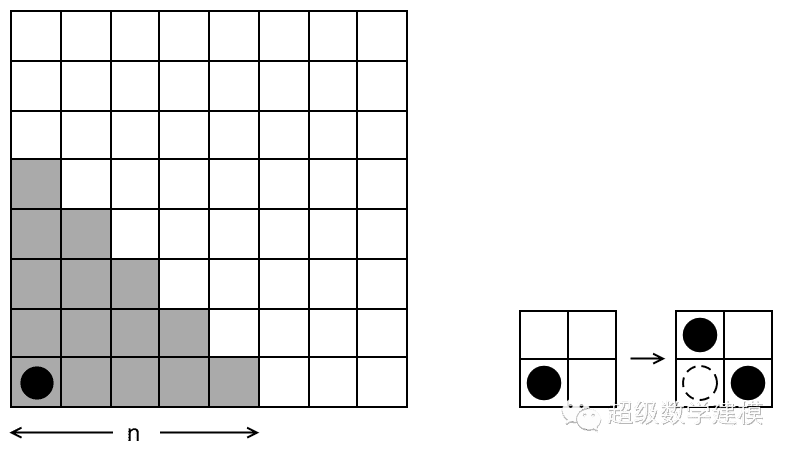
有一个无限大的棋盘，棋盘左下角有一个大小为 n 的阶梯形区域，其中最左下角的那个格子里有一枚棋子，如左图所示。你每次可以把一枚棋子“分裂”成两枚棋子，分别放在原位置的上边一格和右边一格。你的目的是通过有限次的操作，让整个阶梯里不再有任何棋子。下图所示的是 n = 2 时的一种解法。我们的问题是：对于那些 n ，这个游戏是有解的？
赶紧带着你的朋友到留言区秀智商吧！！！
也欢迎分享给爱烧脑的伙伴们！
相关推荐
-
猎杀潜航1中文版下载(猎杀潜航下载地址)
二战大部分时间，作为轴心国伙伴的德国和日本相互猜忌，实际上是各自为战，并没有实质性的合作。1944年底，二战临近尾声，纳粹德国四面受敌渐渐招架不住。为了摆脱困境，希特勒决定向日本提供高技术支持，试图帮助日军重新夺取太平洋战场制空权，从而也减轻自身的压力。1944年12月5日，德国大型潜艇U864号搭
-
steam错误代码118win11(steam显示错误代码118)
相信很多人都会碰到这个问题，打开steam就弹出这个错误，无法进入设置进行交易，甚至个人资料都不行。这个其实还是很容易进行修复的，我们需要修复工具steamcommunity由于系统缺少服务，点击这款工具启动服务就能解决了！非常的简单，只需要点以下就修复了，不需要重新下载游戏。每个人的系统不一样，所
-
水下迷宫怎么找小龙女(如何进入水下迷宫)
答：1水下副本属于迷宫类型，建议先查攻略。避水珠是消耗品，每进入一次水下副本，就消耗一颗避水珠。珍珠店使用珍珠作为代金币。珍珠从福禄寿副本的禄星副本里面获取。2水下副本每个小场景里面都有一个类似于机关的珍珠，攻击它，让它变亮。水下迷宫攻击6个房间，进入顺序可以先进入从右向左的龙卷风3次，然后再从左到
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请通知我们，一经查实，本站将立刻删除。