高考数学选择题题型(高考选择题题型)-百科学社

做选择题除了用了知识点之外，还可以用选择题本身的漏洞做题。大家记住一点，所有选择题，题目或者答案必然存在暗示点：

1)有选项。利用选项之间的关系，我们可以判断答案是选或不选。如两个选项意思完全相反，则必有正确答案。

2)答案只有一个。大家都有这个经验，当时不明白什么道理，但是看到答案就能明白，由此选项将产生暗示。

3)题目暗示。选择题的题目必须得说清楚。大家在审题过程中，是必须要用到有效的讯息的，题目本身就给出了暗示。

4)利用干扰选项做题。选择题除了正确答案外，其他的都是干扰选项，除非是乱出的选项，否则都是可以利用选项的干扰性做题。一般出题者不会随意出选项，总是和正确答案有点关系，或者是可能出错的结果，我们就可以借助这个命题过程得出正确的结论。

5)选择题只管结果，不管中间过程，因此在解题过程中可以大胆的简化中间过程。

6)选择题必须考察课本知识，做题过程中，可以判断和课本哪个知识相关？那个选项与这个知识点无关的可立即排除。因此联系课本知识点做题。

8)选择题必须保证考生在有限时间内可以做出来的，因此当大家花很多时间想不对的时候，说明思路错了。选择题必须是由一个简单的思路构成的。

知道了这个前提之后，就来看看一些技巧↓↓↓

1. 排除法：利用已知条件和选项所提供的信息，从四个选项中剔除掉三个错误的答案，从而达到正确选择的目的。这是一种常用的方法，尤其是答案为定值，或者有数值范围时，取特殊点代入验证即可排除。

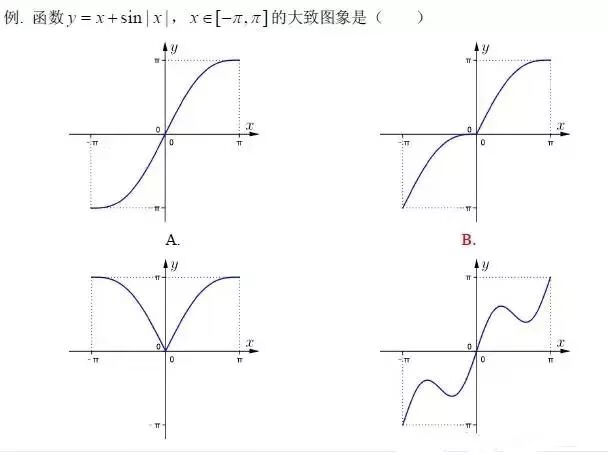
y=x为奇函数，y=sin|x|为偶函数，奇函数＋偶函数为非奇非偶函数，四个选项中，只有B选项为非奇非偶函数，凭此一点排除ACD。

2. 特殊值检验法：对于具有一般性的数学问题，在解题过程中，可以将问题特殊化，利用问题在某一特殊情况下不真，则它在一般情况下不真这一原理，达到去伪存真的目的。值得注意的是，特殊值法常常也与排除法同时使用。

代入特殊值0，显然符合，排除AD；代入x=－1显然不符，排除C。

3. 极端性原则：将所要研究的问题向极端状态进行分析，使因果关系变得更加明显，从而达到迅速解决问题的目的。极端性多数应用在求极值、取值范围、解析几何、立体几何上面，很多计算步骤繁琐、计算量大的题，采用极端性去分析，就能瞬间解决问题。

直接取AB⊥CD的极端情况，取AB中点E，CD中点F，连结EF，令EF⊥AB且EF⊥CD，算出的值即最大值，无须过多说明。

4. 顺推破解法：利用数学定理、公式、法则、定义和题意，通过直接演算推理得出结果的方法。如下题，根据题意，依次将点代入函数及其反函数即可。

5. 逆推验证法(代答案入题干验证法)：将选项代入题干进行验证，从而否定错误选项而得出正确答案的方法。常与排除法结合使用。

代入x=0，显然符合，排除AD；代入x=－1显然不符，排除C。选B。

6. 正难则反法：从题的正面解决比较难时，可从选项出发逐步逆推找出符合条件的结论，或从反面出发得出结论，在做排列组合或者概率类的题目时，经常使用。

7. 数形结合法：由题目条件，做出符合题意的图形或图象，借助图形或图象的直观性，经过简单的推理或计算，从而得出答案的方法。数形结合的好处就是直观，甚至可以用量角尺直接量出结果来。

作图后直接得出选项A符合

8. 递推归纳法：通过题目条件进行推理，寻找规律，从而归纳出正确答案的方法，例如分析周期数列等相关问题时，就常用递推归纳法。

9. 特征分析法：对题设和选择项的特点进行分析，发现规律，归纳得出正确判断的方法。

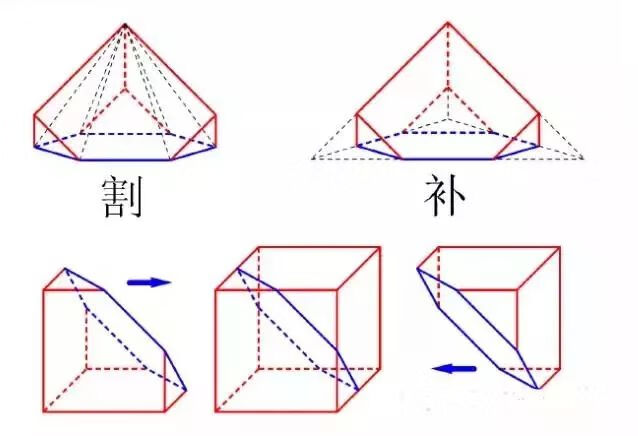
如果不去分析该几何体的特征，直接用一般的割补方法去做，会比较头疼。细细分析，其实该几何体是边长为2的正方形体积的一半，如此这般，不用算都知道选C。

10. 估算法：有些问题，由于题目条件限制，无法(或没有必要)进行精准的运算和判断，此时只能借助估算，通过观察、分析、比较、推算，从面得出正确判断的方法。

这种没办法解的方程，只能通过估算求解。当然，在可以使用计算器的情况下，估算也可以也精确，使用TABLE或者SOLVE功能，可计算约等于0.42

但是！

平时做题时不要过分依赖于技巧！

如果，你在“猜”选择题时经常出现要么都感觉对、要么有两个实在难以抉择的情况，这只能说你需要的不是答题技巧，而是你的基础不扎实，对所学知识掌握不全面，这是大忌！此时就应该去补补基础知识了~

免责声明

    以上文章转载自互联网，文章内容仅供参考，不构成建议，也不代表百科学社赞同其观点。如有侵权请联系755934052@qq.com，提供原文链接地址以及资料原创证明，本站将会立即删除

高考数学选择题题型(高考选择题题型)