本文出自数学家阿哈罗尼（Ron Aharoni）《小学算术教什么，怎么教》一书。他用一些实例来告诉我们整数的由来以及发明“数”的意义。

上帝创造整数；余皆人力所为。

——克罗内克

数为什么是发明出来的？

我九岁的女儿喜欢在生日卡上写：「给你很多、很多、很多……的爱」，几乎塞满半页的「很多」。

也许几千年前还没发明数字的时候，就是用这种方法代替计数。穴居人不会说「3颗石头」，而是说「石头、石头、石头。」

为什么要发明数字的理由现在就很清楚了：为求精简！我女儿其实不必写半页「很多」，其实只需写「一百次那多的爱。」

不过我也得承认效果并非相同。

在三年级的某班上，我想让小朋友了解使用数字会多省力，就讲了一个故事给他们听。不过我会先提醒他们：「我讲的故事发生在某种东西还没有发明的时候，你们要猜猜看那是什么？」

穴居人出外打猎一整天，回到洞穴后对老婆说：「我带回来兔子、兔子、兔子。」老婆回答说：「谢谢你、谢谢你丶谢谢你」

（来自书中插图）

小朋友一下就猜对答案：那是发生在发明数字以前的事。现在我们会简短的说「3只兔子」，或「3个谢谢你」（更口语的说法是，多谢）。

有4只免子时，讲「兔子、兔子、兔子、兔子」不会有困难，但是想想看，如果穴居人带回来的是100只兔子！数字节省了许多气力，它使用了数学精简的三要素：表示法、推广（4可以用来算兔子、铅笔、汽车）、秩序——知道每类东西有几个，提供了有关世界本质的讯息，也创造了某种秩序。

因为同类型的单位可以反复使用，所以才产生了数字1、2、3……。它们的发明是那么样的自然，因而称为「自然数」。所有其他类型的数，像是分数，负数，实数、复数等等，都在更晚的时代才发明，而且因为与日常生活相去较远，所以比较不那么自然。

在本书中，单单出现「数」这个字时，指的就是自然数，也就是（正）整数。

为什么数在数学里扮演核心角色？

随便问一个路人：数学是什么，答案恐怕都会包含「数」——数学在处理数字。专业数学家知道这样说是不准确的，因为有些数学领域，例如几何，并不直接处理数字。但是通俗的看法也包含了相当的真理：数在数学里确实有特殊的角色，数几乎出现在每一个数学领域里，至少也会间接出现。为什么这样？

我们前面说过，数学把基本的思维过程抽象化。数之所以扮演如此核心的角色，是因为数是把所有过程里最基本的部分抽象出来的结果：也就是从世界梳理出个别物件。人们认定世界的一部分，把它跟其余部分分离当成独立单元，再赋予名称：例如「苹果」、「椅子」、「家庭」，这就是字词创造出来的过程，以及数字「1」的起源——「1颗苹果」、「1张椅子」、「1个家庭」。把同类型单元加以重复，就产生了自然数：「2颗苹果、3颗苹果……」。

带单位的数与纯粹的数

「我本来打算有一个丈夫七个子女，但后来把数目搞颠倒了。」

——拉娜·透纳

虽然拉娜·透纳说明了数的重要性，然而最首要的其实是单位，也就是这个数是在计算什么。

数的概念确实源自于带着单位的数，也就是用来计数物件有多少。抽象的数诞生较迟，因为是后来才发现数的重要性质，例如四则运算的结果与单位的选取并不相干：苹果也好，椅子也好，2+3＝5总是对的。

所以人就实践抽象了：从4颗苹果与4张椅子的启发，发明了「纯粹」的数，也就是没有单位的数字：4。纯粹的数可以用来表达含有任何真实物质的命题。

这是导出抽象的具体例子，由此可知我们应该先教带单位的数，再教纯粹的数，换句话说，应该通过计数实际存在的东西来教学生数字概念。一年级生应该尽量多做计数，那是建立数字概念的唯一途径，教室柽应该摆放钮釦、弹珠、冰棒棍，吸管，而且计数的时候，一定要同时说出单位，回答「我们有几枝铅笔时？」，不要只说「4」，应该说「4枝铅笔」。

教单位的第一课

以下的内容是对于进行单位的第一课时该怎么教的建议。先警告班上同学，你要给奇怪的指令，等到抓住他们的注意力之后，就要求一位小朋友：「给我2」。在接下去的讨论，你会教导小朋友在你说「2」时，一定要说「2个什么」。

集合

第一个算术运算既不是加法也不是减法，而是会生出数字的运算——也就是定义单位。

换句话说，就是把一个物质从世界中分离，赋予名字，再定义成为「单位」，从此单位就能重复使用。

事实上，定义出单位是比数的发明还更基本的操作，也可以用来建立其他数学概念，特别是建立集合的概念，而集合是仅次于数的最重要数学概念。集合的概念是从发现若干东西放在一起能形成新单位而来的，这个新单位就叫做「集合」。几个人放在一起成为「家」的集合，5位球员放在一起组成篮球队的集合。

这项操作在数的十进位系统里最为显著。十个个体组织起来成为新单位叫「十」，十个「十」可以用来创造另一个单位叫「百」。

顺序

数不仅用来计数东西，也可用来把东西排序：「第一，第二，第三……」数目之间可以比大小，然后按照大小排序。当数目a小于数目b，我们写成：a＜b。例如，3＜5。有些小朋友觉得不容易记住符号的方向，所以大部分教科书会教记忆法：在符号「＜」有大开口的那边写大的数目。符号「＜」只用在纯粹的数之间，我们不会写「3颗苹果＜5颗苹果」，因为在一年级使用数目时都带着单位，所以最好用「更多」与「更少」，或更正式一点的「大于」与「小于」，而把符号「＜」留到二年级再用。

有一项基本工具可以帮助孩子想象数的顺序，它的名称是「数线」，就是在一条直线上，按照相等距离标示出数字。这是用来表示纯粹数之间的顺序，所以也应该延迟到二年级才学习。一年级生还在计数阶段，等距离标示、数与直线相连、把数跟点当做同样东西等等，对一年级生都嫌太抽象了。

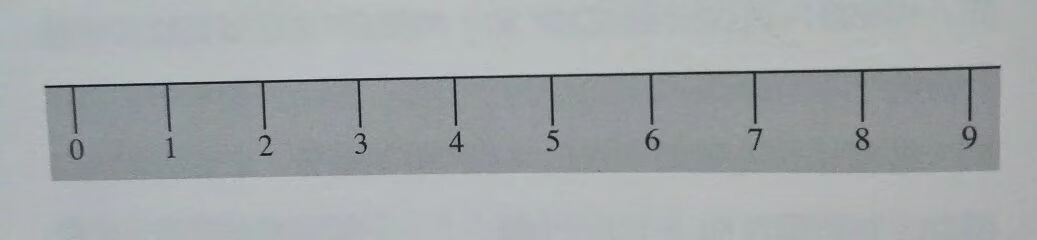
（来自书中插图）