矿工最近做项目的时候，遇到一个需求，甲方巴巴要求对一个双层结构的指标体系进行评分，结果

一顿Google猛如虎，

有用结果不过五。

大刀阔斧瞎捣鼓，

自研算法出权数。

路过壮士请留步，

动动手指点关注。

在统计理论和实践中，权重是表明各个评价指标（或者评价项目）重要性的权数，表示各个评价指标在总体中所起的不同作用。在具体业务场景中，最常见的评价指标类型分为：单层指标体系和双层指标体系。

单层指标体系

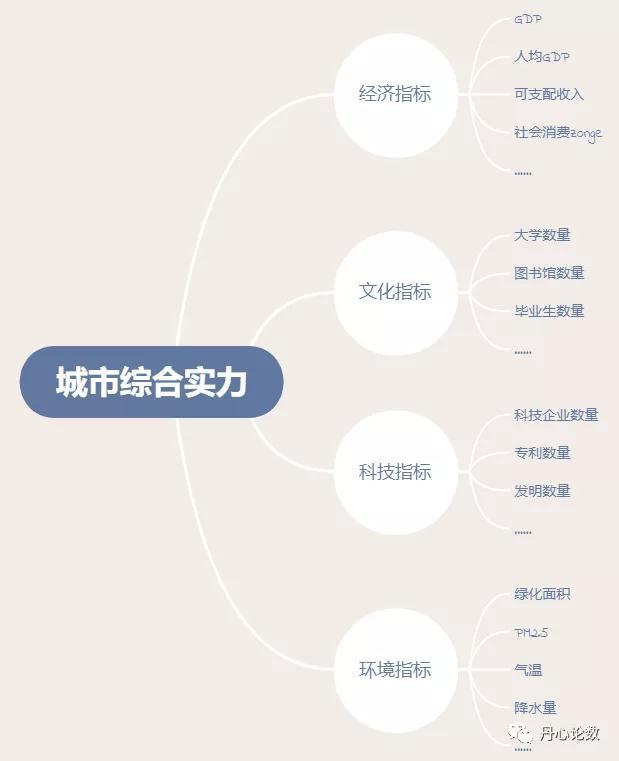
双层指标体系

针对两类指标体系本文提供以下三大类五种赋权算法进行指标赋权。

主观赋权法：g_one

客观赋权法：变异系数法、熵权法、主成分分析法

集成赋权法：乘法集成

对于各个算法具体原理，可自己Google和百度一下，这里只简单介绍一下算法本质，主观赋权法顾名思义就是人为拍脑袋进行赋权，最早的算法是德尔菲法又名专家法，简单粗暴直接拍脑袋定权重，后期又出现层次分析法和g_one法，后者是前者的优化和改进版本，也是本文所用的方法，这两类算法的原理是相较于对指标进行整体比较，人更容易做出两两比较的理性判断，所以“专家”只需要拍定每两个指标之间的相对重要性，就可推导得到整体指标体系中各个指标的相对重要性。

客观赋权法，则是根据数据反映的信息量，进行赋权，信息量越大的数据其对应指标权重越大，根据信息量的衡量方式不同就衍生出了不同的客观赋权方法：熵权法利用信息熵来衡量数据反映的信息量，变异系数法则是用变异系数反映信息量，主成分分析法则是利用各个指标对主成分的贡献度作为衡量指标。

集成赋权法：将主观赋权与客观赋权得到的权重进行集成，根据计算方法不同，可分为：加法集成、乘法集成等

理论讲完，下面开始撸码。

# g1赋权法
 def g_one(r_list):
        r_list.append(1)
        r_list.reverse()
        wei_list = np.cumprod(r_list)
        w_list = list(wei_list/sum(wei_list))
        w_list.reverse()
        return w_list

# 熵权法
def entropy_weight(x):
        x = x.apply(lambda x: ((x - np.min(x)) / (np.max(x) - np.min(x))))
        index_list = x.columns.tolist()
        rows, cols = x.shape
        k = 1.0 / np.log(rows)
        x = np.array(x)
        lnf = [[None] * cols for i in range(rows)]
        lnf = np.array(lnf)
        for i in range(0, rows):
            for j in range(0, cols):
                if x[i][j] == 0:
                    item = 0.0
                else:
                    p = x[i][j] / x.sum(axis=0)[j]
                    item = np.log(p) * p * (-k)
                lnf[i][j] = item
        lnf = pd.DataFrame(lnf)
        new_data = lnf
        redund = 1 - new_data.sum(axis=0)
        w = [[None] * 1 for i in range(cols)]
        for j in range(0, cols):
            wj = redund[j] / sum(redund)
            w[j] = wj 
        return w

#  变异系数法
 def var_weight(data):
        x = data
        index_list = data.columns.tolist()
        x = x.apply(lambda x: ((x - np.min(x)) / (np.max(x) - np.min(x))))
        x_mean = x.mean(axis=0)
        x_std = x.std(ddof=0)
        x_cof_var = x_std/x_mean
        sum_x_cof_var = x_cof_var.sum()
        x_wi = x_cof_var/sum_x_cof_var
        return x_wi

 # 主成分分析法
 from sklearn.decomposition import PCA
 def pca_weight(data):
        index_list = data.columns.tolist()
        x = np.array(data)
        pca = PCA(n_components=2)
        pca.fit(x)
        component = pca.components_
        variance_ratio = pca.explained_variance_ratio_
        component = abs(component.T)
        for i in range(0,2):
            component[:, i] = variance_ratio[i]*component[:, i]
        a = pd.DataFrame(component)
        b = a.sum(axis=1)
        c = b/b.sum(axis=0)
        c = c.to_frame()
        return c