.jpg)
导数是函数值相对于自变量的瞬时变化率，求导数是一个取极限的过程。对于一个连续且可导的函数，其导数的定义如下
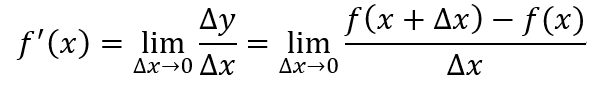
函数可导的前提是函数必须连续，对于连续函数，有下列等式成立
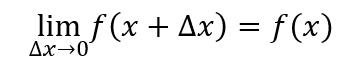
上式是函数在x处连续的定义。结合连续函数的定义和极限的运算性质，我们接下来推导导数运算法则。
两个函数相加的导数
假设F(x)为两个可导函数的和
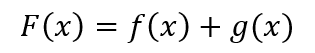
那么根据导数定义，F(x)的导数为
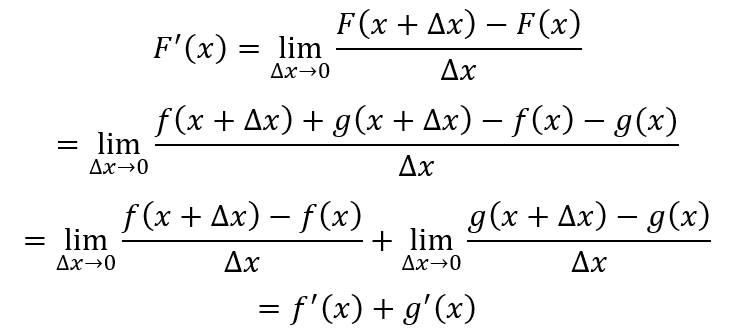
即两个可导函数的和的导数等于导数的和，导数运算减法同理。
两个函数乘积的导数
假设G(x)为两个可导函数的和
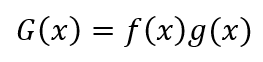
根据导数定义，G(x)的导数为
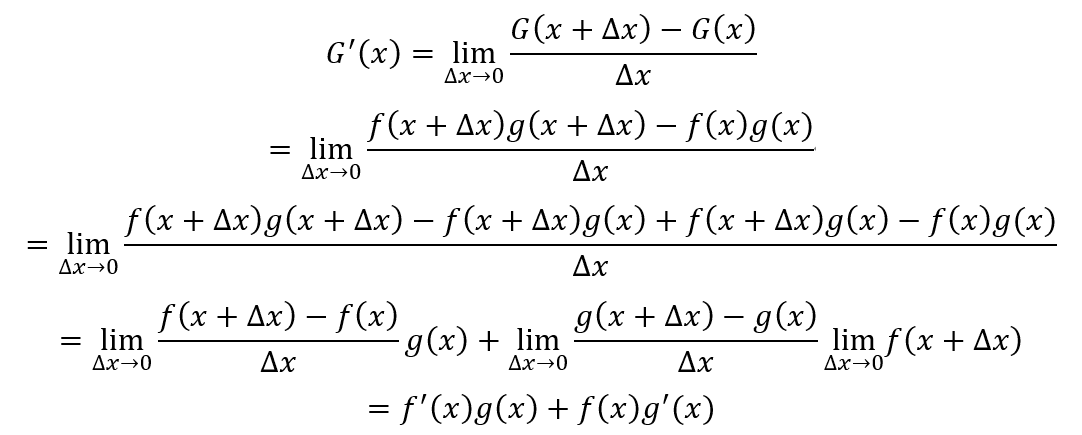
两个可导函数的乘积的导数的结果为
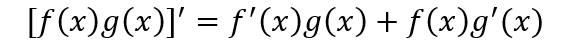
两个函数的比值的导数
假设H(x)为两个可导函数的比值
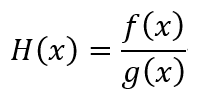
根据导数定义，那么H(x)的导数为
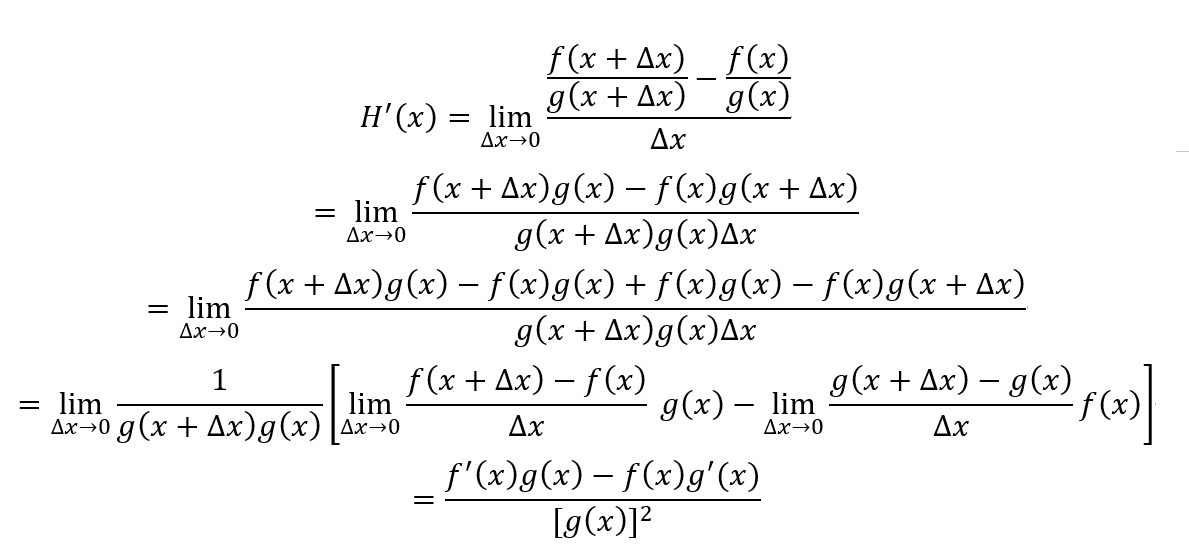
两个可导函数的比值的导数结果为
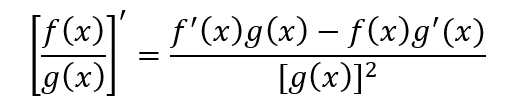
掌握推导过程可以帮助理解导数的定义和运算。
本文由小朱与数学原创，欢迎关注，带你一起长知识！
相关推荐
-
大学生当兵真的好吗(在校大学生当兵的利弊)
现在当兵基本都是以大学生为主，初中生和高中生当兵的情况越来越少，以后会退出历史的舞台，这是社会发展必然的趋势，现在大学生当兵有“前途”吗？小编认为还是非常有前途，主要是这两大原因，大学生当兵的“政策福利”和在部队的发展“机遇”。一、保留学籍，这个绝对是一个很好的政策，高考结束可以保留入学资格去当兵，
-
yesman男装(yes madam)
小伙伴们在没有正式开始学习英语之前，估计都有听到过“yes,sir”或者“yes,madam”吧，当年在电影和港剧里出现超级多啊！（不小心暴露年龄啦）那大家非常熟悉的“yes”，在英语口语中还有什么其他的搭配用法呢？我们赶紧来看看！1）yes-manYes是“是”，man是“人”，那“yes-man
-
世界屋脊是哪个地方(世界屋脊指什么)
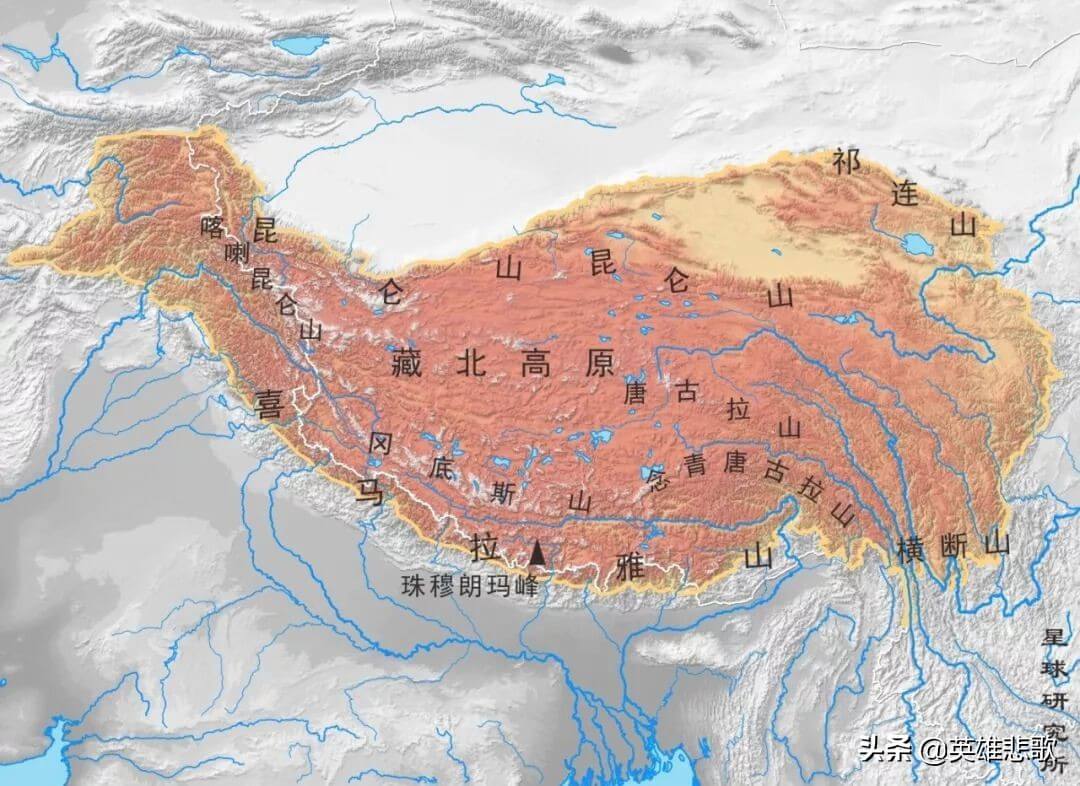
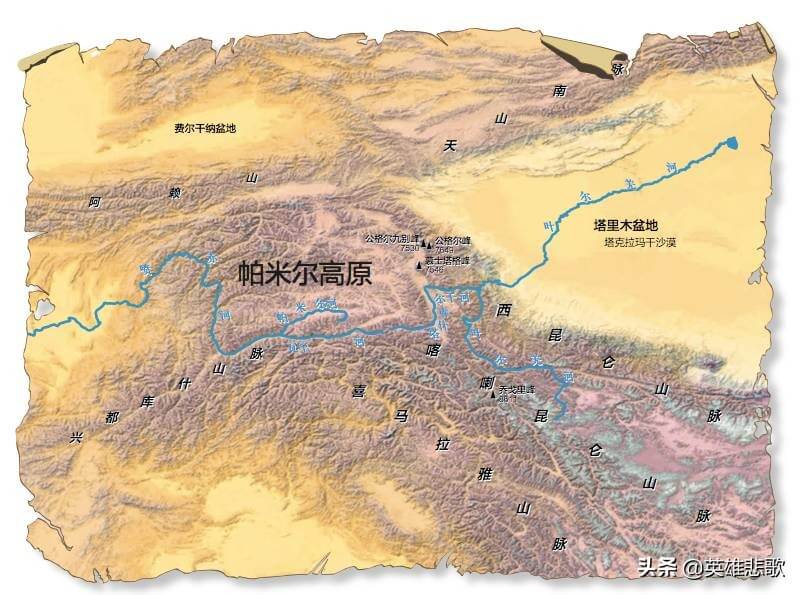
比面积，青藏高原地跨西藏、青海、新疆以及尼泊尔、印度、不丹，面积高达250万平方公里，而帕米尔高原只是位于新疆西南喀什以西、与巴控克什米尔、印度、阿富汗和塔吉克斯坦交界处的一块高原，面积10万平方公里。青藏高原地形图青藏高原是中国最大的高原，但不是世界上最高的高原。严格意义上来说，青藏高原才是高 原
-
留学机构是干嘛的(哪个留学机构比较靠谱)
留学培训是一种有组织留学知识、语言技能的培训，在使学生了解出国考试的必备能力及准备方法的同时，为学生能够尽快适应到国外的语言环境、文化风俗，更好的在国外学习和生活作准备。培训的内容主要有留学语言培训、出国留学的相关申请、国外文化的了解和学习等几个方面。具体的内容根据学生的需求进一步的调整。按培训的时
-
西北政法大学是几本学校(西亚斯毕业证不被承认)
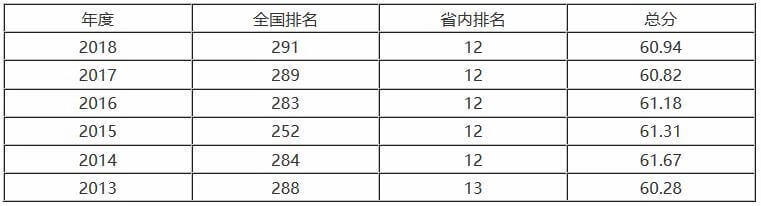
今天小编介绍的这所一本院校是5大政法院校之一，不是211和双一流高校，位于西安，地理位置上吃亏，这所大学就是西北政法大学。西北政法大学简称“西法大”，1937年创办，位于陕西西安。学校是一所由陕西省政府和中央共同创办的政法高等学府。学校是“五院四系”之一和省部共建高校。学校有2个校区，分别是雁塔校区
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请通知我们，一经查实，本站将立刻删除。