.jpg)
三边都相等的三角形叫等边三角形，等边三角形是一种特殊的等腰三角形．拥有等腰三角形所有的性质，并且具有自己特有的性质。
1.等边三角形的性质
等边三角形三个内角都相等，并且每一个内角都等于60°；等边三角形是轴对称图形，具有三条对称轴。
例题1：如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H．（1）求证：△BCE≌△ACD；（2）求证：FH∥BD．
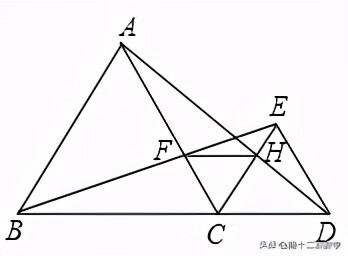
第1问：先根据△ABC和△CDE都是等边三角形得出BC=AC，CE=CD，∠BCA=∠ECD=60°，再由SAS定理即可得出△BCE≌△ACD；
第2问：由（1）知△BCE≌△ACD，可知∠CBF=∠CAH，BC=AC，再由ASA定理可知△BCF≌△ACH，可得出CF=CH，根据∠FCH=60°，可知△CHF为等边三角形，进而可得出结论．
这也是“手拉手模型”基本的模型图，里面包含的结论远远不止这两个。如果将其中一个等边三角形绕着点C进行旋转，也会得到一系列的结论。
2.等边三角形的判定
常用的方法有：
（1）三条边都相等的三角形是等边三角形；
（2）三个角都相等的三角形是等边三角形；
（3）有一个角是60°的等腰三角形是等边三角形．
例题2：如图，在△ABC中，∠A=120°，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，点E，F为垂足，求证：△DEF是等边三角形．
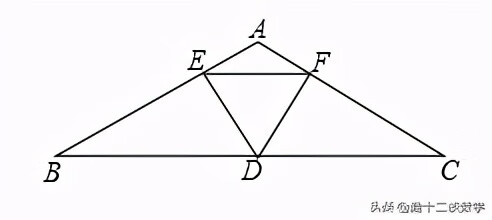
分析：由∠A=120°，AB=AC，易得∠B=∠C=30°，从而得∠EDF=60°，因为D是BC的中点，易证△BDE≌△CDF，由全等三角形的性质得DE=DF，由等边三角形的判定得△DEF是等边三角形．
本题主要考查了等腰三角形的性质，全等三角形的性质及判定定理，等边三角形的判定，找出等边三角形的判定条件是解答此题的关键。在证明等边三角形时，第三种判定方法用得比较多。
3.含30°的直角三角形
在直角三角形中，如果有一个锐角是30°，那么它所对的直角边等于斜边的一半。这个定理的前提条件是“在直角三角形中”，是证明直角三角形中一边等于另一边（斜边）的一半的重要方法之一，通常用于证明边的倍数关系和计算线段的长度，这个直角三角形中，三边的比为：1：2：根号3.
例题3：已知：如图，等边△ABC中，AE=CD，AD、BE相交于点P，BQ⊥AD于Q．求证：BP=2PQ．
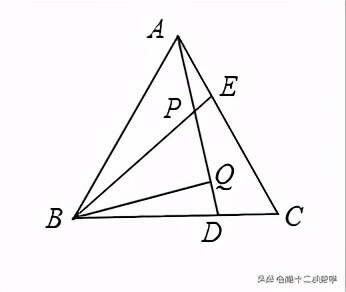
分析：根据全等三角形的判定方法SAS可证得△BEC≌△ADB，根据各角的关系及三角形内角、外角和定理可证得∠BPQ=60°，即可得结论．
本题主要考查了等边三角形的性质、三角形外角的性质、含30°直角三角形的性质及全等三角形的判定与性质。
相关推荐
-
学汽修去哪家好(学汽修好不好)
汽修学校哪家好?近几年很多高校毕业生都面临着就业难的问题，究其原因不过就是高校毕业生没有实践经验和专业技能，所以在就业的时候我们需要的不仅仅是学历，还有很大的一部分在于技能，来北方汽修学校就能让你技能学历双丰收，就业有保障。汽修学校哪家好? 在就业难的今天，技能已经成为了就业的优势，应用型人才
-
党执政兴国的第一要务是谁提出来的(党执政兴国的什么)
光明日报记者 钟超辉煌的事业，总能在历史的风云中找到起点；壮阔的征程，总能在岁月的长河中溯源初心。2002年11月8日，中国共产党第十六届全国代表大会在北京召开。这次大会确立了“三个代表”重要思想为党的指导思想，科学制定了全面建设小康社会的宏伟纲领，顺利实现了党的中央领导集体的新老交替，为中国在新世
-
嘉应学院咋样(嘉应学院是名校吗)
[ - ] 学院 · 基本信息中 文 名：嘉应学院创办时间：1913年类 别：公办大学学校类型：综合属 性：全日制普通本科院校所属地区：广东梅州主管部门：广东省录取批次：本科学校代码：10582学 费：5800/学年宿 舍 费：750-1300元/学年（学费、宿舍费等信息参考自《广东省2020普通高
-
疫情英雄人物(抗击疫情中的英雄人物有哪些)
陈薇（前左二）向志愿者讲解疫苗知识。 张振威摄（新华社发）去年9月8日，全国抗击新冠肺炎疫情表彰大会在北京人民大会堂隆重举行，中国工程院院士、军事科学院军事医学研究院研究员陈薇获颁“人民英雄”国家荣誉称号奖章。在新冠肺炎疫情防控的阻击战中，陈薇带领团队作出重大贡献：新冠肺炎疫情发生后，闻令即动，带领
-
中专女生适合什么职业(中专的女生为什么那么好上)
中专学历是比较低一些，但这并不代表只有中专学历的你就完全没办法找到适合的、心仪的好工作，今天小编想要以适合中专女生的工作作为例子跟大家分享一下，希望能够让大家更好的去了解到底有什么备选的工作。客服工作，一般来说，女性的声线都是比较柔和的，所以做客服、在跟大家沟通和交流的过程中，会因为语气比较柔和，让
版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容， 请通知我们，一经查实，本站将立刻删除。